二分算法

二分算法基本框架

class Solution {
    public int searchInsert(int[] nums, int target) {
        int left = 0,right=nums.length-1,ans=right+1;
        while(left<=right){
        int mid = (left + right)/2;
        if(nums[mid]>=target){
          ans=mid;
          right=mid-1;}
        else 
        left=mid+1;
        }
    return ans;
}

分析二分查找的一个技巧是：不要出现 else，而是把所有情况用 else if 写清楚，这样可以清楚地展现所有细节。本文都会使用 else if，旨在讲清楚，读者理解后可自行简化。

其中 … 标记的部分，就是可能出现细节问题的地方，当你见到一个二分查找的代码时，首先注意这几个地方。后文用实例分析这些地方能有什么样的变化。

另外声明一下，计算 mid 时需要技巧防止溢出，即 mid=left+(right-left)/2。本文暂时忽略这个问题。

一、寻找一个数（基本的二分搜索）

这个场景是最简单的，可能也是大家最熟悉的，即搜索一个数，如果存在，返回其索引，否则返回 -1。

int binarySearch(int[] nums, int target) {
    int left = 0;
    int right = nums.length - 1; // 注意

    while(left <= right) {
        int mid = (right + left) / 2;
        if(nums[mid] == target)
            return mid;
        else if (nums[mid] < target)
            left = mid + 1; // 注意
        else if (nums[mid] > target)
            right = mid - 1; // 注意
        }
    return -1;
}

1. 为什么 while 循环的条件中是 <=，而不是 < ？

答：因为初始化 right 的赋值是 nums.length-1，即最后一个元素的索引，而不是 nums.length。

这二者可能出现在不同功能的二分查找中，区别是：前者相当于两端都闭区间 [left, right]，后者相当于左闭右开区间 [left, right)，因为索引大小为 nums.length 是越界的。

我们这个算法中使用的是前者 [left, right] 两端都闭的区间。这个区间其实就是每次进行搜索的区间，我们不妨称为「搜索区间」。

什么时候应该停止搜索呢？当然，找到了目标值的时候可以终止：

1 2	if(nums[mid] == target) return mid;

但如果没找到，就需要 while 循环终止，然后返回 -1。那 while 循环什么时候应该终止？搜索区间为空的时候应该终止，意味着你没得找了，就等于没找到嘛。

while(left <= right) 的终止条件是 left == right + 1，写成区间的形式就是 [right + 1, right]，或者带个具体的数字进去 [3, 2]，可见这时候搜索区间为空，因为没有数字既大于等于 3 又小于等于 2 的吧。所以这时候 while 循环终止是正确的，直接返回 -1 即可。

while(left < right) 的终止条件是 left == right，写成区间的形式就是 [left, right]，或者带个具体的数字进去 [2, 2]，这时候搜索区间非空，还有一个数 2，但此时 while 循环终止了。也就是说这区间 [2, 2] 被漏掉了，索引 2 没有被搜索，如果这时候直接返回 -1 就是错误的。

当然，如果你非要用 while(left < right) 也可以，我们已经知道了出错的原因，就打个补丁好了：

//...
while(left < right) {
    // ...
}
return nums[left] == target ? left : -1;

详解解析看 [https://www.cnblogs.com/mxj961116/p/11945444.html]

leetcode_剑指 Offer II 069. 山峰数组的顶部

二分题解

class Solution {
    public int peakIndexInMountainArray(int[] arr) {
    int left = 0 , rigth = arr.length-1,ans = 0;
    while(left<=rigth)
    {
        int mid = (left+rigth)/2;
        if(arr[mid]>arr[mid+1])
        {ans = mid;
        rigth = mid-1;}
        else
        left = mid+1;

    }
    return ans;
    }
}

leetcode_35

35. 搜索插入位置

题解

class Solution {
    public int searchInsert(int[] nums, int target) {
        int left = 0,right=nums.length-1,ans=right+1;
        while(left<=right){
        int mid = (left + right)/2;
        if(nums[mid]>=target){
          ans=mid;
          right=mid-1;}
        else 
        left=mid+1;
        }
    return ans;
        }
}

33. 搜索旋转排序数组

题解

class Solution {
    public int search(int[] nums, int target) {
        int left = 0, right = nums.length - 1,ans = 0;
        while(left <= right)
        {
            int mid=(left+right);
            if(nums[mid] > nums[right]){
                if(target > nums[mid])
                {
                    left = mid+1;
                }
                else if(target < nums[mid])
                {
                    right = mid-1;
                }
                else 
                    ans = mid;
            }
            if(nums[mid] <nums[right]){
                if(target<nums[mid])
                {
                    left=mid+1;
                }
                else if(target > nums[mid])
                {
                    right=mid-1;
                }
                else
                    ans=mid;
            }
    }
    return ans;
}
}

剑指 Offer II 069. 山峰数组的顶部

题目

符合下列属性的数组 arr 称为 山峰数组（山脉数组） ：

arr.length >= 3
存在 i（0 < i < arr.length - 1）使得：
arr[0] < arr[1] < ... arr[i-1] < arr[i]
arr[i] > arr[i+1] > ... > arr[arr.length - 1]
给定由整数组成的山峰数组 arr ，返回任何满足 arr[0] < arr[1] < ... arr[i - 1] < arr[i] > arr[i + 1] > ... > arr[arr.length - 1] 的下标 i ，即山峰顶部。

 

示例 1：

输入：arr = [0,1,0]
输出：1
示例 2：

输入：arr = [1,3,5,4,2]
输出：2
示例 3：

输入：arr = [0,10,5,2]
输出：1
示例 4：

输入：arr = [3,4,5,1]
输出：2
示例 5：

输入：arr = [24,69,100,99,79,78,67,36,26,19]
输出：2
 

提示：

3 <= arr.length <= 104
0 <= arr[i] <= 106
题目数据保证 arr 是一个山脉数组
 

进阶：很容易想到时间复杂度 O(n) 的解决方案，你可以设计一个 O(log(n)) 的解决方案吗？

我写的想法第一次就想到for循环遍历写出了O（n）的学法

int peakIndexInMountainArray(int* arr, int arrSize){
    int temp=0;
    for(;temp<arrSize-1;temp++){
        if(arr[temp]>arr[temp+1])
        break;
    }
    return temp;
}

三叶姐姐的解法

二分
往常我们使用「二分」进行查值，需要确保序列本身满足「二段性」：当选定一个端点（基准值）后，结合「一段满足 & 另一段不满足」的特性来实现“折半”的查找效果。

但本题求的是峰顶索引值，如果我们选定数组头部或者尾部元素，其实无法根据大小关系“直接”将数组分成两段。

但可以利用题目发现如下性质：由于 arr 数值各不相同，因此峰顶元素左侧必然满足严格单调递增，峰顶元素右侧必然不满足。

因此以峰顶元素为分割点的 arr 数组，根据与前一元素/后一元素的大小关系，具有二段性：

峰顶元素左侧满足 arr[i-1] < arr[i]arr[i−1]<arr[i] 性质，右侧不满足
峰顶元素右侧满足 arr[i] > arr[i+1]arr[i]>arr[i+1] 性质，左侧不满足
因此我们可以选择任意条件，写出若干「二分」版本。

代码：

class Solution {
    // 根据 arr[i-1] < arr[i] 在 [1,n-1] 范围内找值
    // 峰顶元素为符合条件的最靠近中心的元素
    public int peakIndexInMountainArray(int[] arr) {
        int n = arr.length;
        int l = 1, r = n - 1;
        while (l < r) {
            int mid = l + r + 1 >> 1;
            if (arr[mid - 1] < arr[mid]) l = mid;
            else r = mid - 1;
        }
        return r;
    }
}

时间复杂度：O(\log{n})O(logn)
空间复杂度：O(1)O(1)
三分和k分

```java
class Solution {

public int peakIndexInMountainArray(int[] arr) {
    int n = arr.length;
    int l = 0, r = n - 1;
    while (l < r) {
        int m1 = l + (r - l) / 3;
        int m2 = r - (r - l) / 3;
        if (arr[m1] > arr[m2]) r = m2 - 1;
        else l = m1 + 1;
    }
    return r;
}

}

作者：AC_OIer
链接：https://leetcode-cn.com/problems/B1IidL/solution/gong-shui-san-xie-er-fen-san-fen-ji-zhi-lc8zl/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。


 

题干

秋天快到啦，天气慢慢凉爽了下来，所以实验室要组织去骊山进行一次野餐活动。

最底层的Lofipure被迫背背包给大家装各种零食，但是实验室的大佬们并不打算轻易放过Lofipure，他们打算把Lofipure的背包装的尽量满

现在知道Lofipure的背包容量为 V（正整数，0 <= V <= 20000），同时有 n 件小零食（0＜n<=30），每个小零食的重量。
现在在 n 个小零食中，任取若干个装入Lofipure的背包内，使得Lofipure背包的剩余空间为最小。借此达到压榨Lofipure的目的。


Input

输入：一个整数v，表示背包容量 一个整数n，表示有n个物品 接下来 n 个整数，分别表示这 n 个物品的各自体积

Output

输出：一个整数，表示背包最小的剩余空间

Sample Input

24
6
8
3
12
7
9
7

1
2
3


Sample Output


看到这道理的第一时刻想的是暴力枚举出所有零食混合装的重量  可复杂度太高 遂放弃。

然后看了一下大佬们的代码

```c++
#include<bits/stdc++.h>
#define int long long
#define MAXN 1000005
using namespace std;
int dp[20005];
signed main()
{
    dp[0]=1;
    int v,n;cin>>v>>n;
    for(int i=1;i<=n;i++)
    {
        int t;cin>>t;
        for(int j=v;j>=t;j--)
            dp[j]|=dp[j-t];
    }
    for(int i=v;i>=0;i--)
    {
        if(dp[i])
        {
            cout<<v-i<<endl;
            return 0;
        }
    }
}

刚开始我用Java实现的时候，


后面经过自己  ~~人眼比对~~ 发现这个错误  发现之后感到不解。

```dp [j]|=dp[j-t]```这个式子用来干嘛的呢

后面经过输出

```java
System.out.println(j+" "+(j-t)+" "+dp[j]+" "+dp[j - t]);

形式一下子就清楚了 dp是为了统计零食能够组成的重量

拿本题例子来说

输入 t = 8 时只有dp[8] = dp[8] | dp[0] 才变成1 这代表着能够组成8的重量

输入 t = 3 时有了dp[11] = dp[11] | dp[11 - 3] dp[3] = dp[3] | dp[0] 这次增加 11（8+3） 3(3+0)l两种可能

输入t = 12时有dp[23] = 1 ,dp[20] = 1 dp[15] =1 dp[12] = 1

输入t = 7时有 dp[22] = 1,dp[22] = 1 dp[19] = 1 dp[18] = 1 dp[15] = 1 dp[10] = 1

。。。。

到最后会使所有能够凑出重量的dp数都为1

从最大的量递减便利当dp[i] 不为0 时也就是为1 代表着这是能够装载着最大的重量直接输出V-i

感叹算法的奇妙与精彩，只恨自己接触晚与学校氛围不好，蹉跎了许久时光。

JAVA版代码

package com.VG;

import java.util.Arrays;
import java.util.Scanner;

public class C {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int V = scanner.nextInt();
        int N = scanner.nextInt();
        int[] dp = new int[200005];
        dp[0] = 1;
        for (int i = 1; i <= N; i++) {
            int t = scanner.nextInt();
            for (int j = V; j >=t ; j--) {
                dp[j] |= dp[j - t];
                System.out.println(j+" "+(j-t)+" "+dp[j]+" "+dp[j - t]);
            }
        }
        for (int i = V; i >= 0 ; i--) {
            if(dp[i]!=0)
            {
                System.out.println(V- i);
                return;
            }
        }

    }
}

快速幂

50. Pow(x, n)

难度中等8

实现 pow(x, n) ，即计算 x 的 n 次幂函数（即，xn）。

示例 1：

1 2	输入：x = 2.00000, n = 10 输出：1024.00000

示例 2：

1 2	输入：x = 2.10000, n = 3 输出：9.26100

示例 3：

1
2
3

输入：x = 2.00000, n = -2
输出：0.25000
解释：2-2 = 1/22 = 1/4 = 0.25

提示：

-100.0 < x < 100.0
-231 <= n <= 231-1
-104 <= xn <= 104

如果要计算2 的 1024 次方我们用朴素算法要乘以1024次算法复杂法O（1024） O（10）

如果每次都平方一下

1	1->2->4->8->16->32->64->128->256->512->1024

时间复杂的为O（log 1024）也就是10

算法板子

class Solution {
    public double myPow(double x, int n) {
        long N = n;
        return N >= 0 ? quickMul(x, N) : 1.0 / quickMul(x, -N);
    }

    public double quickMul(double x, long N) {
        if (N == 0) {
            return 1.0;
        }
        double y = quickMul(x, N / 2);
        return N % 2 == 0 ? y * y : y * y * x;
    }
}

class Solution {
    public double myPow(double x, int n) {
        long N = n;
       double ans = quickMul(x,N);
        if(N>=0) return ans;
        else return 1.0/ans;
    }

    public double quickMul(double x, long N) {
        if (N == 0) {
            return 1.0;
        }
        double y = quickMul(x, N / 2);
        if(N%2==0) return y*y;
        else return y*y*x;
    }
}

进阶

372. 超级次方

难度中等

你的任务是计算 ab 对 1337 取模，a 是一个正整数，b 是一个非常大的正整数且会以数组形式给出。

示例 1：

1 2	输入：a = 2, b = [3] 输出：8

示例 2：

1 2	输入：a = 2, b = [1,0] 输出：1024

示例 3：

1 2	输入：a = 1, b = [4,3,3,8,5,2] 输出：1

示例 4：

1 2	输入：a = 2147483647, b = [2,0,0] 输出：1198

提示：

1 <= a <= 231 - 1
1 <= b.length <= 2000
0 <= b[i] <= 9
b 不含前导 0

class Solution {
    static final int MOD = 1337;

    public int superPow(int a, int[] b) {
        int ans = 1;
        for (int i = b.length - 1; i >= 0; --i) {
            ans = (int) ((long) ans * pow(a, b[i]) % MOD);
            a = pow(a, 10);
        }
        return ans;
    }

    public int pow(int x, int n) {
        int res = 1;
        while (n != 0) {
            if (n % 2 != 0) {
                res = (int) ((long) res * x % MOD);
            }
            x = (int) ((long) x * x % MOD);
            n /= 2;
        }
        return res;
    }
}

作者：LeetCode-Solution
链接：https://leetcode-cn.com/problems/super-pow/solution/chao-ji-ci-fang-by-leetcode-solution-ow8j/

回溯问题

解决一个回溯问题,实际上就是一个决策树的遍历过程，需要思考三个问题

路径：也就是已经做出的选择
选择列表：也就是你当前可以做的选择
也就是到达策树底层，无法再做选择的条件。

回溯算法框架

result = []
def backtrack(路径, 选择列表):
    if 满足结束条件:
        result.add(路径)
        return
    
    for 选择 in 选择列表:
        做选择
        backtrack(路径, 选择列表)
        撤销选择

核心在于for循环里面的递归，在递归调用之前做选择，在递归调用之后撤销选择。

例子1 全排列问题

有n个数每个数都只能用一次求出所有能排列的可能性。全排列个数为n!个

PS：为了简单清晰起见，我们这次讨论的全排列问题不包含重复的数字。

如果已知有多少个数的情况下，我们通常可以使用n层for循环暴力遍历所有数

例如3个数我们可以暴力写法为

for(int i = 0;i < n;i++)
    for(int j = 0;j < n;j++)
        for(int k = 0;k < n;k++)
        {
			if(i!=j && i!=k && j!=k)
            {
                // 1 2 3   1 3 2   2 1 3   2 3 1  3 2 1  3 1 2
				list.add(nums[i]);
                list.add(nums[j]);
                list.add(nums[k]);
                res.add(list);
            }
        }

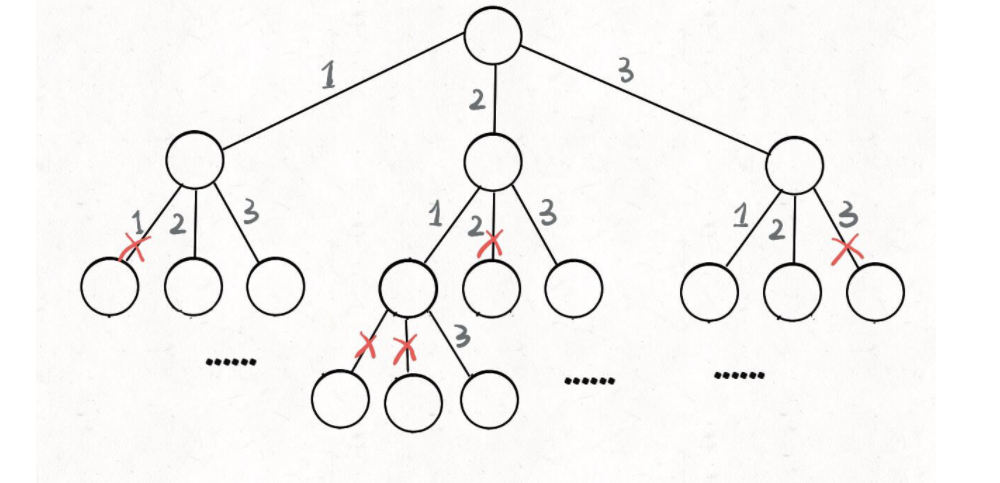
回溯数如下图所示，只要从根遍历这棵树，记录路径下的数字，其实就是所有的全排列，我们不妨把这棵树称之为回溯算法的决策树

为什么叫决策树呢，顾名思义，每次遍历的时候都需要做决策来去避开那些已经走过的路。

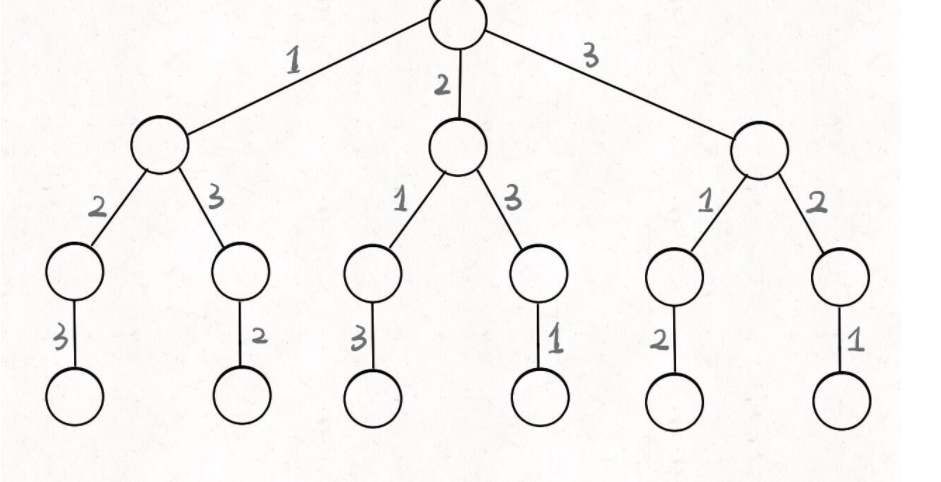
现在可以解答开头的几个名词：[2] 就是「路径」，记录你已经做过的选择；[1,3] 就是「选择列表」，表示你当前可以做出的选择；「结束条件」就是遍历到树的底层，在这里就是选择列表为空的时候。

如果明白了这几个名词，可以把「路径」和「选择」列表作为决策树上每个节点的属性，比如下图列出了几个节点的属性：

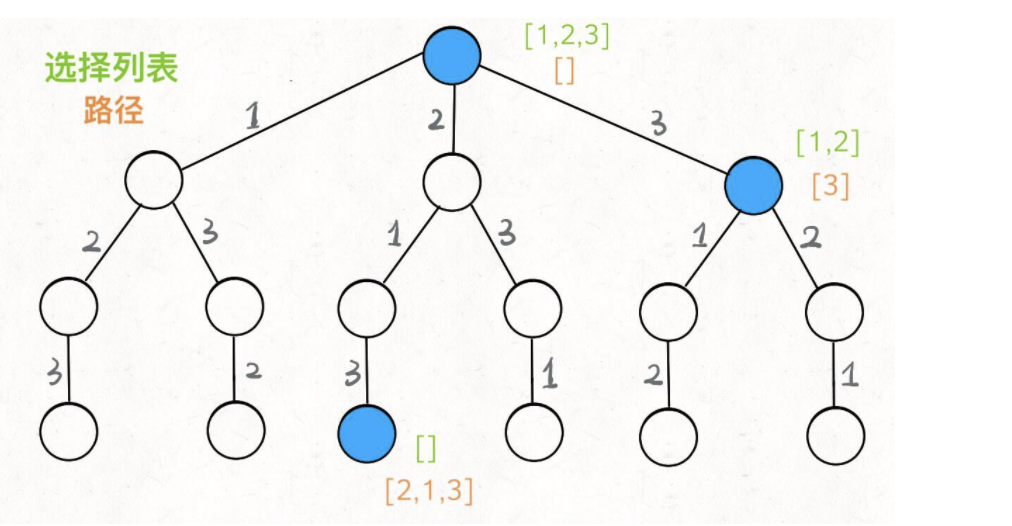
我们定义的backtrack函数就是指针一样，在这棵树上游走，同时要正确维护每个节点的属性，每当走到树的底层，其路径就是一个全排列。

再进一步，如何遍历一颗树，

void traverse(TreeNode root) {
    for (TreeNode child : root.childern)
        // 前序遍历需要的操作
        traverse(child);
        // 后序遍历需要的操作
}

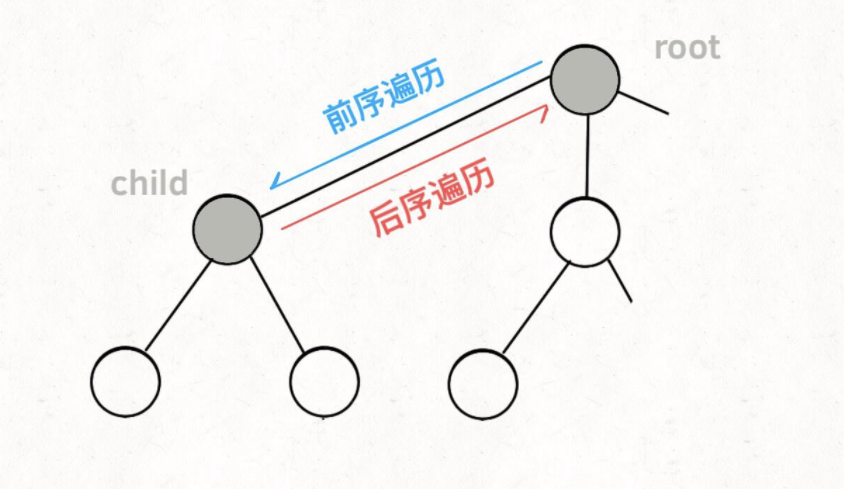
前序遍历的代码在进入某一个节点之前的那个时间点执行，后序遍历代码在离开某个节点之后的那个时间点执行。

回想我们刚才说的，「路径」和「选择」是每个节点的属性，函数在树上游走要正确维护节点的属性，那么就要在这两个特殊时间点搞点动作：

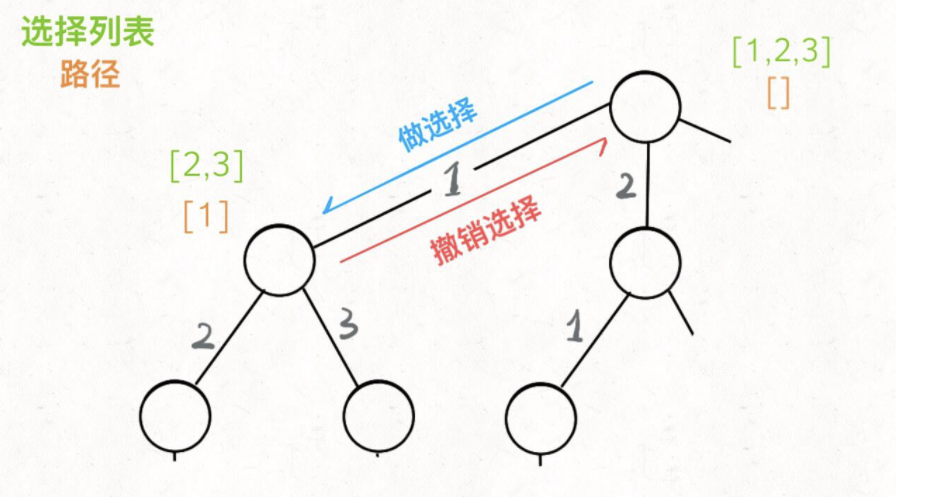
回溯代码核心框架

for 选择 in 选择列表:
    # 做选择
    将该选择从选择列表移除
    路径.add(选择)
    backtrack(路径, 选择列表)
    # 撤销选择
    路径.remove(选择)
    将该选择再加入选择列表

我们只要在递归之前做出选择，在递归之后撤销自己的选择，就能得到每个节点的选择路径和列表。

全排列代码

List<List<Integer>> res = new LinkedList<>();

/* 主函数，输入一组不重复的数字，返回它们的全排列 */
List<List<Integer>> permute(int[] nums) {
    // 记录「路径」
    LinkedList<Integer> track = new LinkedList<>();
    backtrack(nums, track);
    return res;
}

// 路径：记录在 track 中
// 选择列表：nums 中不存在于 track 的那些元素
// 结束条件：nums 中的元素全都在 track 中出现
void backtrack(int[] nums, LinkedList<Integer> track) {
    // 触发结束条件
    if (track.size() == nums.length) {
        res.add(new LinkedList(track));
        return;
    }
    
    for (int i = 0; i < nums.length; i++) {
        // 排除不合法的选择
        if (track.contains(nums[i]))
            continue;
        // 做选择
        track.add(nums[i]);
        // 进入下一层决策树
        backtrack(nums, track);
        // 取消选择
        track.removeLast();
    }
}

我们这里稍微做了些变通，没有显式记录「选择列表」，而是通过 nums 和 track 推导出当前的选择列表：

通过contains函数来判断该数是否已经被使用。

至此，我们就通过全排列问题详解了回溯算法的底层原理。当然，这个算法解决全排列不是很高效，应为对链表使用 contains 方法需要 O(N) 的时间复杂度。有更好的方法通过交换元素达到目的，但是难理解一些，这里就不写了，有兴趣可以自行搜索一下。

但是必须说明的是，不管怎么优化，都符合回溯框架，而且时间复杂度都不可能低于 O(N!)，因为穷举整棵决策树是无法避免的。这也是回溯算法的一个特点，不像动态规划存在重叠子问题可以优化，回溯算法就是纯暴力穷举，复杂度一般都很高。

明白了全排列问题，就可以直接套回溯算法框架了，下面简单看看 N 皇后问题。

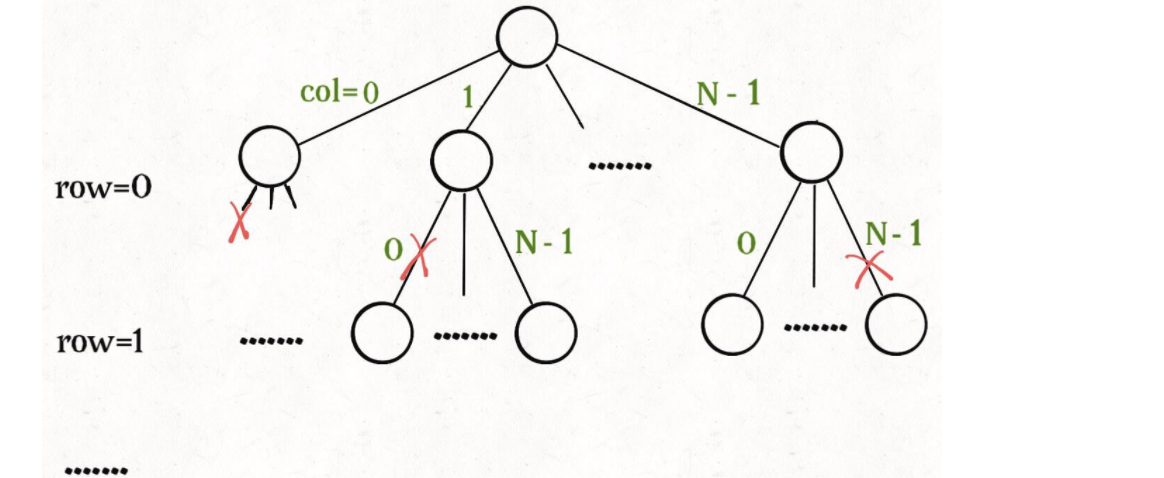
例子2 N皇后问题

题意

给你一个N*N的棋盘，，让你放置 N 个皇后，使得它们不能互相攻击。

PS：皇后可以攻击同一行、同一列、左上左下右上右下四个方向的任意单位。

这个问题本质上跟全排列问题差不多，决策树的每一层表示棋盘上的每一行；每个节点可以做出的选择是，在该行的任意一列放置一个皇后。

vector<vector<string>> res;

/* 输入棋盘边长 n，返回所有合法的放置 */
vector<vector<string>> solveNQueens(int n) {
    // '.' 表示空，'Q' 表示皇后，初始化空棋盘。
    vector<string> board(n, string(n, '.'));
    backtrack(board, 0);
    return res;
}

// 路径：board 中小于 row 的那些行都已经成功放置了皇后
// 选择列表：第 row 行的所有列都是放置皇后的选择
// 结束条件：row 超过 board 的最后一行
void backtrack(vector<string>& board, int row) {
    // 触发结束条件
    if (row == board.size()) {
        res.push_back(board);
        return;
    }
    
    int n = board[row].size();
    for (int col = 0; col < n; col++) {
        // 排除不合法选择
        if (!isValid(board, row, col)) 
            continue;
        // 做选择
        board[row][col] = 'Q';
        // 进入下一行决策
        backtrack(board, row + 1);
        // 撤销选择
        board[row][col] = '.';
    }
}

IsValid()函数

/* 是否可以在 board[row][col] 放置皇后？ */
bool isValid(vector<string>& board, int row, int col) {
    int n = board.size();
    // 检查列是否有皇后互相冲突
    for (int i = 0; i < n; i++) {
        if (board[i][col] == 'Q')
            return false;
    }
    // 检查右上方是否有皇后互相冲突
    for (int i = row - 1, j = col + 1; 
            i >= 0 && j < n; i--, j++) {
        if (board[i][j] == 'Q')
            return false;
    }
    // 检查左上方是否有皇后互相冲突
    for (int i = row - 1, j = col - 1;
            i >= 0 && j >= 0; i--, j--) {
        if (board[i][j] == 'Q')
            return false;
    }
    return true;
}

函数 backtrack 依然像个在决策树上游走的指针，通过 row 和 col 就可以表示函数遍历到的位置，通过 isValid 函数可以将不符合条件的情况剪枝：

某种程度上说，动态规划的暴力求解阶段就是回溯算法。只是有的问题具有重叠子问题性质，可以用 dp table 或者备忘录优化，将递归树大幅剪枝，这就变成了动态规划。而今天的两个问题，都没有重叠子问题，也就是回溯算法问题了，复杂度非常高是不可避免的。

参考链接：https://leetcode-cn.com/problems/permutations/solution/hui-su-suan-fa-xiang-jie-by-labuladong-2/

26. 删除有序数组中的重复项

这题典型的双指针一个指针是用来遍历另外一个用来存储

class Solution {
    public int removeDuplicates(int[] nums) {
        int t = 0;
        for (int i = 0; i < nums.length; i ++ ) {
            if (i == 0 || nums[i] != nums[i - 1]) 
            {
                nums[t] = nums[i];
                t++;
            }
        }
        return t;
    }
}

i用来遍历数组而t用来存储新的数组

通用解法拓展

class Solution {
    public int removeDuplicates(int[] nums) {
        int n = nums.length;
        if (n <= 1) return n;   
        return process(nums, 1, nums[n - 1]);
    }
    int process(int[] nums, int k, int max) {
        int idx = 0; 
        for (int x : nums) {
            if (idx < k || nums[idx - k] != x) nums[idx++] = x;
            if (idx - k >= 0 && nums[idx - k] == max) break;
        }
        return idx;
    }
}

作者：AC_OIer
链接：https://leetcode-cn.com/problems/remove-duplicates-from-sorted-array/solution/shua-chuan-lc-jian-ji-shuang-zhi-zhen-ji-2eg8/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

507. 完美数

两种方法

方法一打表

我试了一下我的打表方式 20分钟还没打出最后一个数

直接搬官方的吧

   class Solution {
   public boolean checkPerfectNumber(int num) {
        return num == 6 || num == 28 || num == 496 || num == 8128 || num == 33550336;
    }
}

方法二枚举

class Solution {
    public boolean checkPerfectNumber(int num) {
        int sum = 0;
        if(num==1) return false;
    for(int i = 1;i <= num/2;i++)
    {
        if(num%i==0)
        sum+=i;
    }
    return sum==num;
    }
}

这个稍微时间稍微长了一点

class Solution {
    public boolean checkPerfectNumber(int num) {
        if (num == 1) return false;
        int ans = 1;
        for (int i = 2; i <= num / i; i++) {
            if (num % i == 0) {
                ans += i;
                if (i * i != num) ans += num / i;
            }
        }
        return ans == num;
    }
}

这个就很快了

同样是枚举别人写的和我写的感觉自己在时间复杂度方法还得加强

20. 有效的括号

给定一个只包括 ‘(‘，’)’，’{‘，’}’，’[‘，’]’ 的字符串 s ，判断字符串是否有效。

有效字符串需满足：

左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。

示例 1：

1 2	输入：s = "()" 输出：true

示例 2：

1 2	输入：s = "()[]{}" 输出：true

示例 3：

1 2	输入：s = "(]" 输出：false

示例 4：

1 2	输入：s = "([)]" 输出：false

示例 5：

1 2	输入：s = "{[]}" 输出：true

提示：

1 2	1 <= s.length <= 104 s 仅由括号 '()[]{}' 组成

题解

class Solution {

  public boolean isValid(String s) {

    int n = s.length();

    if (n % 2 == 1) {

      return false;

    }



    Map<Character, Character> pairs = new HashMap<Character, Character>() {{

      put(')', '(');

      put(']', '[');

      put('}', '{');

    }};

    Deque<Character> stack = new LinkedList<Character>();

    for (int i = 0; i < n; i++) {

      char ch = s.charAt(i);

      if (pairs.containsKey(ch)) {

        if (stack.isEmpty() || stack.peek() != pairs.get(ch)) {

          return false;

        }

        stack.pop();

      } else {

        stack.push(ch);

      }

    }

    return stack.isEmpty();

  }

}

先就s字符串的长度奇数还是偶数进行判断

如果长度是奇数直接返回false 因为不满足闭合条件

367. 有效的完全平方数

第一次直接想的就是暴力遍历

class Solution {
    public boolean isPerfectSquare(int num) {
        for(int i = 1 ;i <= num/2 ; i++)
        {
            if(i*i == num)
            return true;
        } 
        if(num == 1)
        return true;
        else
        return false;
    }
}

样例是全过了但是超时了

class Solution {
    public boolean isPerfectSquare(int num) {
        for(int i = 1 ;i <= num/2 ; i++)
        {
            if(num / i == i && num % i == 0) 
            return true;
             if (num / i < i) return false;
        } 
        if(num == 1 ||num==4)
        return true;
        else
        return false;
    }
}

后面参考评论区

速度是以除代乘速度大大提升。

class Solution {
    public boolean isPerfectSquare(int num) {
        for(int i = num / 2 + 1;i >= 1; i--){
            if(num == i * i) return  true;
        }
        return false;
    }
}

这是第一版的改进从后面开始遍历提升下速率数越大越明显

二分法

class Solution {
    public boolean isPerfectSquare(int num) {
      int low = 1;
      int high = num;
      while(low <= high){
          int mid = low + (high - low) / 2;
          int t = num / mid;
          if(t == mid){
              if(num % mid==0) return true;
              low = mid+1;}
          else if(t<mid)
          {
              high = mid-1;
          }
          else{
              low = mid+1;
          }
          }
      return false;
    }
}

数学方法

所有平方数都是可以由奇数和构成的

1=1 4=1+3 9=1+3+5

则只需要每次从1开始减每次加2 以num>0为判断条件

class Solution {
    public boolean isPerfectSquare(int num) {
       int ans=1;
       while(num > 0)
       {
           num -= ans;
           ans += 2;
       }
       return num==0;
    }
}

在一个平衡字符串中，’L’ 和 ‘R’ 字符的数量是相同的。

给你一个平衡字符串 s，请你将它分割成尽可能多的平衡字符串。

注意：分割得到的每个字符串都必须是平衡字符串，且分割得到的平衡字符串是原平衡字符串的连续子串。

返回可以通过分割得到的平衡字符串的最大数量。

示例 1：

输入：s = “RLRRLLRLRL”
输出：4
解释：s 可以分割为 “RL”、”RRLL”、”RL”、”RL” ，每个子字符串中都包含相同数量的 ‘L’ 和 ‘R’ 。
示例 2：

输入：s = “RLLLLRRRLR”
输出：3
解释：s 可以分割为 “RL”、”LLLRRR”、”LR” ，每个子字符串中都包含相同数量的 ‘L’ 和 ‘R’ 。
示例 3：

输入：s = “LLLLRRRR”
输出：1
解释：s 只能保持原样 “LLLLRRRR”.
示例 4：

输入：s = “RLRRRLLRLL”
输出：2
解释：s 可以分割为 “RL”、”RRRLLRLL” ，每个子字符串中都包含相同数量的 ‘L’ 和 ‘R’ 。

提示：

1 <= s.length <= 1000
s[i] = ‘L’ 或 ‘R’
s 是一个平衡字符串

1221. 分割平衡字符串

在一个 平衡字符串 中，'L' 和 'R' 字符的数量是相同的。

给你一个平衡字符串 s，请你将它分割成尽可能多的平衡字符串。

注意：分割得到的每个字符串都必须是平衡字符串，且分割得到的平衡字符串是原平衡字符串的连续子串。

返回可以通过分割得到的平衡字符串的 最大数量 。

 

示例 1：

输入：s = "RLRRLLRLRL"
输出：4
解释：s 可以分割为 "RL"、"RRLL"、"RL"、"RL" ，每个子字符串中都包含相同数量的 'L' 和 'R' 。
示例 2：

输入：s = "RLLLLRRRLR"
输出：3
解释：s 可以分割为 "RL"、"LLLRRR"、"LR" ，每个子字符串中都包含相同数量的 'L' 和 'R' 。
示例 3：

输入：s = "LLLLRRRR"
输出：1
解释：s 只能保持原样 "LLLLRRRR".
示例 4：

输入：s = "RLRRRLLRLL"
输出：2
解释：s 可以分割为 "RL"、"RRRLLRLL" ，每个子字符串中都包含相同数量的 'L' 和 'R' 。
 

提示：

1 <= s.length <= 1000
s[i] = 'L' 或 'R'
s 是一个 平衡 字符串

题解

class Solution {
    public int balancedStringSplit(String s) {
        int n = s.length();
        int j=0,ans=0;
        for(int i = 0 ; i < n ; i++ )
        {
            if (s.charAt(i)=='R')
            {
                j++;
            }
            if (s.charAt(i)=='L')
            {
                j--;
            }
            if(j==0)
            {
                ans++;
                }
        }
    return ans;
    }
}

453. 最小操作次数使数组元素相等

给你一个长度为 n 的整数数组，每次操作将会使 n - 1 个元素增加 1 。返回让数组所有元素相等的最小操作次数。

示例 1：

输入：nums = [1,2,3]
输出：3
解释：
只需要3次操作（注意每次操作会增加两个元素的值）：
[1,2,3]  =>  [2,3,3]  =>  [3,4,3]  =>  [4,4,4]

示例 2：

1 2	输入：nums = [1,1,1] 输出：0

解析

每一步除了最大的那个数不加1 相等于最大的数减1 参考相对运动理解

每一次操作总和都会-1

那么最后的结果肯定是n个最小数

那么

1	return sum - min * n;

即可得到结果

利用for each语句遍历数组

找出数组里面最小的数和总和sum

for (int i : nums) {
            min = Math.min(min, i);
            sum += i;
        }

题解

class Solution {
    public int minMoves(int[] nums) {
        int n = nums.length;
        int min = nums[0], sum = 0;
        for (int i : nums) {
            min = Math.min(min, i);
            sum += i;
        }
        return sum - min * n;
    }
}

这是一个记录成长的博客

算法积累

二分算法

35. 搜索插入位置

33. 搜索旋转排序数组

剑指 Offer II 069. 山峰数组的顶部

50. Pow(x, n)

372. 超级次方

回溯问题

例子1 全排列问题

全排列代码

例子2 N皇后问题

题意

26. 删除有序数组中的重复项

507. 完美数

20. 有效的括号

367. 有效的完全平方数

1221. 分割平衡字符串

453. 最小操作次数使数组元素相等